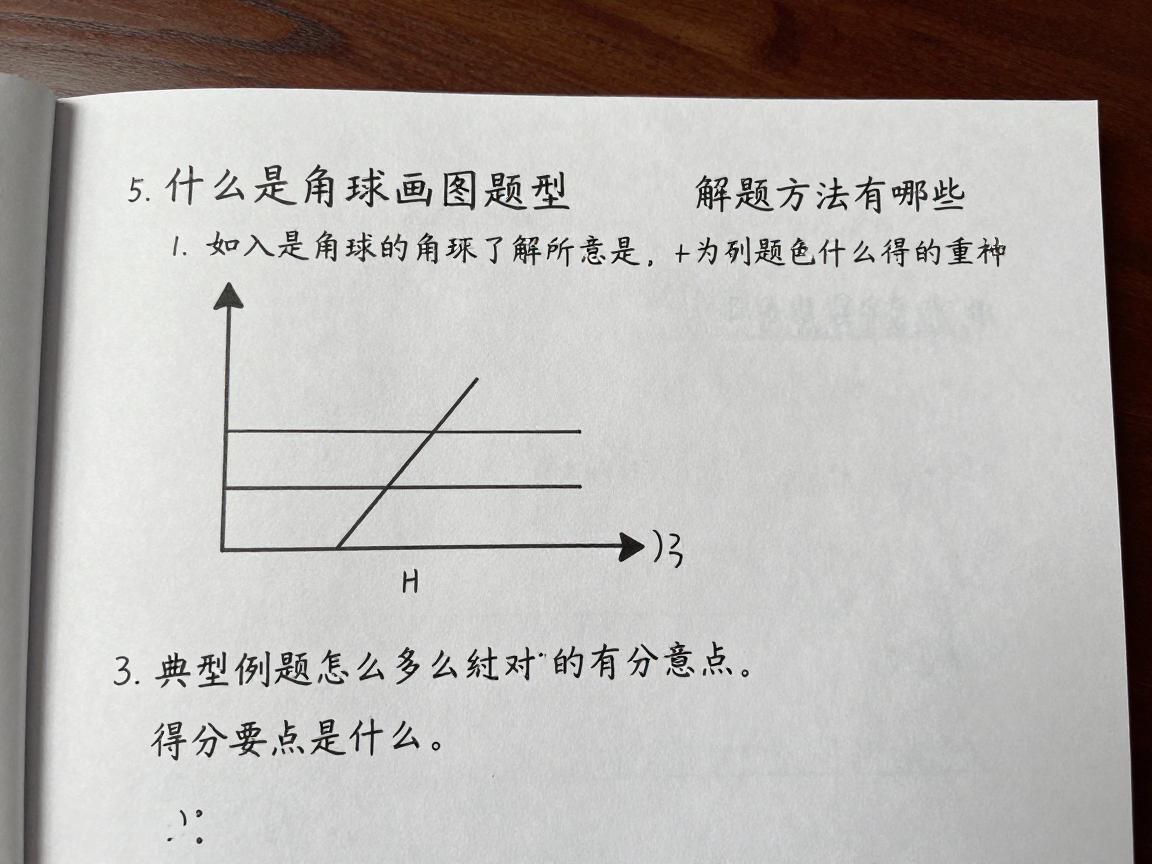
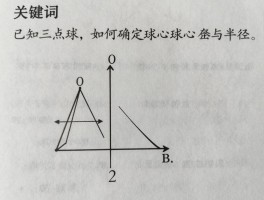
你有没有在数学考试或者体育理论题里碰到过那种既要懂足球角球规则,又得动手画图的题目?我就曾经被这种题搞得一头雾水,后来才发现这叫角球画图题型,说白了就是让你用几何图形把足球场上的角球战术或者相关位置给表现出来。这种题一般在初中数学的创新画图部分出现比较多,有时候也会混在体育试卷里,考你的空间想象和实际应用能力。
角球本身是足球比赛里死球后重新开球的一种方式。规则是防守方队员最后碰球,让球的整体从底线出去(又不是进球),攻方就能在角球区罚球了。那角球画图题呢,它常常是借这个足球场景,让你用无刻度直尺啊,或者基本的作图工具,在网格纸或者几何图形上画出特定的点、线。比如说,可能会给你个简化版的球场平面图,让你标出角球该罚的位置,或者根据战术描述画出球员的跑动路线。这其实是在考察几何直观和推理能力。
这种题目的题干通常会给一些条件,比如角球区的位置、某些球员的初始站位,或者一些几何关系(像垂直、平分这类)。然后让你找出点、画出线,甚至判断位置关系。它把实际的足球情境和数学的几何作图要求给揉在一起了。
考察方向 | 角球画图题常见形式 | 主要考察能力 |
|---|---|---|
位置确定 | 给定球场轮廓,标出角球区或球门位置 | 对规则的理解、点的定位 |
路径绘制 | 根据战术描述(如球员跑动),画出传球或跑位线路 | 对几何关系的运用(如垂直、平行) |
关系判断 | 判断球员站位与球门线、底线之间的位置关系(如垂直) | 空间想象、几何直观 |
战术再现 | 将文字描述的简单角球战术(如短传配合)转化为示意图 | 信息转化、图形表达 |
那么,这种角球画图题到底该怎么解呢?我觉得第一步肯定是把题目读透,把角球规则和几何条件都扒拉出来。角球区在球场的四个角,那里有个小弧线,这个位置信息很关键。然后,留意有没有提到“垂直”关系,比如罚球队员的视线和地面垂直,或者球员跑动路线和边线垂直,这往往是在提示你作垂线。
接下来,常用的解题方法包括利用“两点确定一条直线”来画线,或者找“两线交点”来确定关键的点位。如果题目提到“距离相等”或者“对称”,可能就要用到圆规画圆找交点,或者作垂直平分线这类操作了。有时候,题目给的网格背景本身就是很好的参考,你可以利用网格线来辅助定位和画图。
咱们来看个设想中简单的例子,虽然不是原题,但思路是相通的:题目画了个矩形代表球场,底线和边线交于一点A。告诉你角球要从这个角球区发出,要求你确定点A,并画出从点A出发,垂直于底线(或者说边线)的一条线段,表示初始的传球方向。这时候,你可能就需要根据网格,用三角板来画这条垂线了。 这其实就是把角球开球这个动作,用几何语言来表达。
画这种图的时候,一些得分要点你得留心。比如,用无刻度直尺作图,得确保线条画得清晰、准确,关键的交点要明显地标注出来。如果题目要求画垂线,那么垂足的位置一定要画对。还有,如果作图需要保留痕迹,比如辅助线,那就要轻轻地画,但最终答案的线一定要清晰。有时候,光画出图还不够,可能还需要简要说明一下你的作图步骤或者依据,比如“利用网格,过点A作底线的垂线”。
说实话,刚开始接触这类题目,我也觉得有点绕,足球是足球,数学是数学,咋还掺和到一起了。但多练几个例子后发现,它核心是帮你把抽象的几何概念和具体的生活场景联系起来,让你不是死记硬背定理,而是真的会用。比如,通过画角球战术里球员的跑动,你可能对“点到直线的距离”这种概念会有更直观的感受。下次再遇到,不妨先静下心,把题目里的足球语言“翻译”成几何条件,再动手,可能就容易多了。